尤力课题组提出一种通用算法高效求解量子多体系统基态简并度
Oct 09 2025
在量子物理研究的众多领域中,基态简并度是一个核心概念,它对于理解相变、拓扑物质和阻挫系统等多体物理现象至关重要。然而,精确计算基态简并度是一个公认的难题,其计算复杂度高于寻找系统基态本身。常见复杂度分类关系如下图所示。
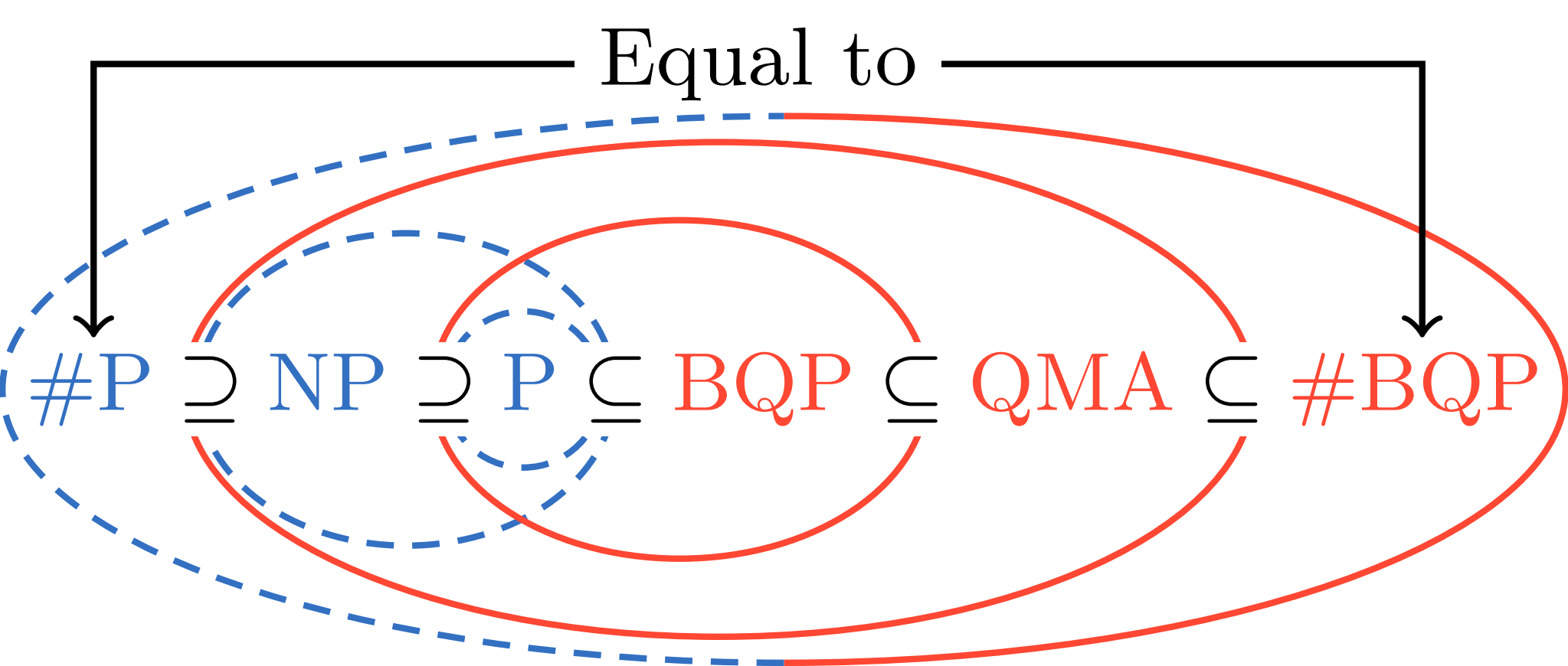
图1 常见复杂度分类关系图。蓝色和红色分别代表经典和量子算法。
P复杂类包括可以在多项式时间内解决的问题;而NP是未确定可否在多项式时间内解决,但是可以在多项式时间内验证的问题。背包问题、质数分解等重要问题都属于NP问题。NP问题被认为不简单于P问题。而#P问题则是在给出NP问题解的基础上找出所有解的个数,#P问题被认为不简单于NP问题。而在量子计算领域,这三个计算复杂度类都有了对应的量子版本,分别对应BQP(bounded-error quantum polynomial time),QMA(quantum Merlin Arthur)和#BQP(sharp BQP)问题。寻找系统基态属于QMA复杂类,而计算基态简并度则属于#BQP复杂类。
近日,清华大学物理系尤力教授课题组提出了一种创新的通用算法,巧妙地将高复杂度的基态简并度“计数”问题,转化为了一个在扩展系统中寻找特殊单个基态的优化问题。该算法的核心是为原系统构建一个“超哈密顿量”(super Hamiltonian),这个新的哈密顿量作用于一个两倍量子比特(或自旋)的扩展系统上。研究证明,这个超哈密顿量的基态,恰好编码了原系统基态简并度的信息。一般而言,量子比特数目翻倍并不会改变问题的复杂度标度,比如著名的肖尔(Shor)算法中需要的比特数也是系统规模的两倍左右。这项工作通过求解一个额外大一倍比特数的系统的基态这一QMA问题,得到了原系统上的基态简并度这一#BQP问题的解的信息,成功搭建了从 QMA 复杂度问题到 #BQP 复杂度问题解的新桥梁。
这项工作受到了审稿人的高度评价,其意义在于,它为所有传统的演化类算法打开了计算基态简并度的大门。研究者只需将现有成熟的求基态算法稍作修改——即将演化对象从原哈密顿量换为超哈密顿量,并将初始状态固定为“真空态”——即可求解出这个特殊的基态,进而通过一次简单的测量便能精确得到原系统的基态简并度。该方法不仅在理论上严谨,而且复杂度与求解原系统基态属于同一类复杂度标度,极具实用价值。并在多个典型物理模型上通过数值模拟演示了其潜在应用,包括一维系统中的相变探测、二维阻挫系统的精确求解、以及真实化学体系的量子线路高效实现等。
该研究成果以“Counting the Ground State Degeneracy by Evolution Methods”为题,于2025年10月6日发表于《物理评论快报》(Physical Review Letters)。清华大学物理系2023届博士毕业生郭臻(已毕业)为该论文的第一作者及通讯作者。该工作得到了国家自然科学基金和科技部量子科学与技术创新计划的支持。
