赵永刚研究组在磁斯格明子包的产生与调控方面取得进展
Jan 06 2025
磁斯格明子是微、纳米尺度上的一种具有类粒子特性的拓扑非平庸自旋结构,能被磁场、电流、电场等多种方式操控,在自旋电子学方面有着重要的应用前景,有望成为下一代信息存储和逻辑运算的载体,引起了广泛的关注。同时斯格明子也涌现出新奇、丰富的物理现象,如拓扑霍尔效应、斯格明子霍尔效应等,具有重要的科学意义。近几年来,随着斯格明子相关研究的深入,探索不同拓扑数的自旋结构以及揭示其三维自旋结构成为研究热点。这其中磁斯格明子包是近几年才在实验上发现的一种拓扑自旋结构。斯格明子包可以理解成内部N个斯格明子被外面一个大的斯格明子(拓扑数与内部斯格明子相反)包围形成,因其可以具有任意高拓扑数Q = N - 1而引人关注,高拓扑数使得其相比于斯格明子可以拥有更高的信息编码自由度,同时斯格明子包为拓扑磁学研究提供了新的平台。目前对斯格明子包的研究主要集中在单相块体材料方面,具有诸多优点的磁性多层膜结构中斯格明子包的研究还有待深入。
最近,清华大学赵永刚研究组利用基于磁控溅射技术生长的典型斯格明子体系[Ta/CoFeB/MgO]×15多层膜结构(图1a),探索出一种在受限结构中产生能在室温、零磁场下稳定的单个斯格明子包的方法。利用微加工得到不同尺寸的微米级受限圆盘阵列(图1b),发现对于合适尺寸的圆盘,利用小角度饱和倾斜磁场磁化后能得到“网状”畴结构,该结构进一步在面外磁场诱导下可逐步转变成斯格明子包结构(图1c),并且在撤去磁场后斯格明子包结构仍能保持稳定。在此基础上,探索了斯格明子包的相关性质,包括斯格明子包拓扑数对受限圆盘尺寸的依赖性(图1d)、宏观磁场驱动下的拓扑数逐级转变(图1e)以及局域磁场调控行为等。通过与北京理工大学的黄厚兵教授合作,利用微磁学仿真分析了受限圆盘的特殊边界条件(边界附近高磁各向异性能密度区域)对于斯格明子包产生和零场稳定性的机制,从能量角度解释了斯格明子包拓扑数对于圆盘尺寸的依赖性,同时分析了厚度方向斯格明子包畴壁手性结构的分布,并进一步探索了不同材料参数下斯格明子包的稳定情况(进而分析该斯格明子包制备方法对于其他材料的适用性),部分模拟结果如图2所示。该工作为磁性多层膜结构中斯格明子包的研究提供了一种有效方法,也将激发后续进一步的研究工作。
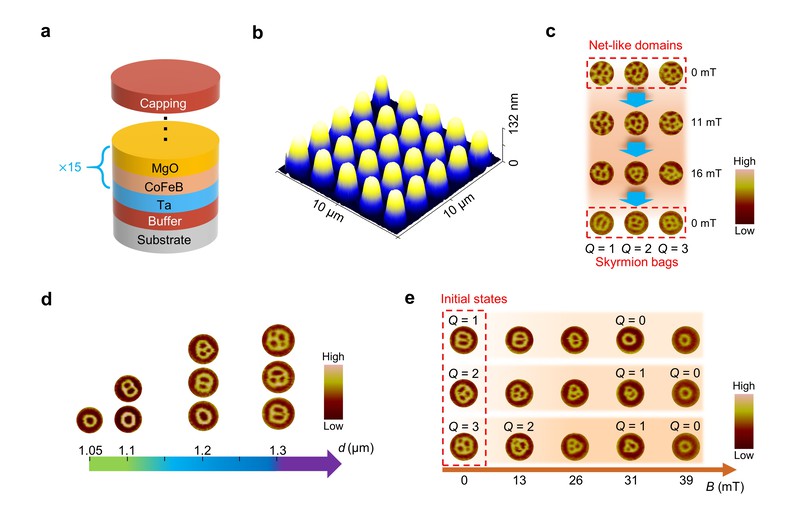
图1 实验结果(磁畴由磁力显微镜MFM成像)。a 样品结构示意图。b 受限圆盘阵列形貌图(原子力显微镜AFM图)。c “网状畴”转变成斯格明子包的过程。d 斯格明子包拓扑数对圆盘尺寸的依赖性。e 磁场驱动斯格明子包拓扑数的逐级转变。
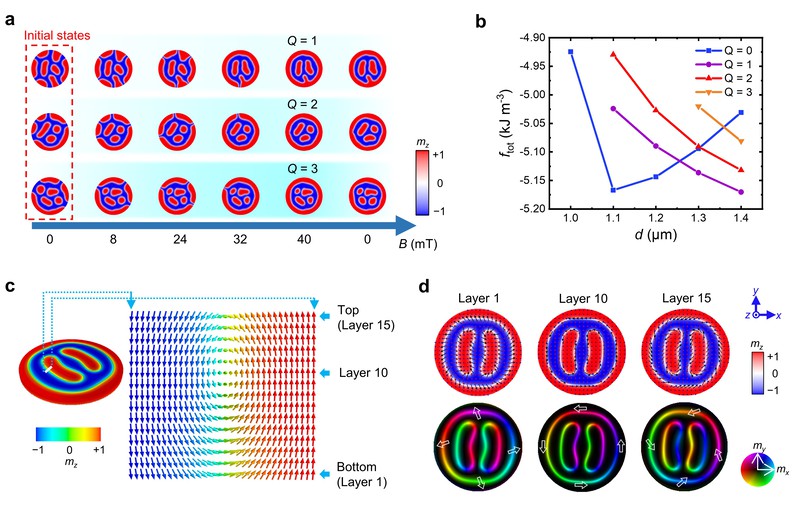
图2 微磁模拟结果。a 模拟“网状畴”转变成斯格明子包的过程。b 从能量角度解释斯格明子包拓扑数对圆盘尺寸的依赖性。c和d 模拟的斯格明子包畴壁手性结构在样品厚度方向的分布。
该研究成果以“Room-temperature creation and conversion of individual skyrmion bags in magnetic multilayered disks”为题于2025年1月2日发表在《自然·通讯》(Nature Communications)上。清华大学物理系赵永刚教授和北京理工大学前沿交叉科学研究院黄厚兵教授为该论文通讯作者;清华大学物理系2019级博士生刘权、北京理工大学前沿交叉科学研究院博士生董守哲、清华大学物理系2018级博士生王雨桐为该论文的共同第一作者。论文合作者包括中国科学院物理研究所蔡建旺研究员、兰州大学柴国志教授、清华大学宋成教授、清华大学江万军副教授、清华大学朱静院士、清华大学南策文院士等。该工作得到了国家自然科学基金、科技部重点专项等项目的支持。
文章链接:https://www.nature.com/articles/s41467-024-55489-z
